Perceiving a 3-dimensional Surface

Throughout this material, we have worked with the sphere and the hypersphere in the form of slices. Though a Flatlander's best conception of a sphere exists "chopped up" into an array of circles (as a stack-diagram is arranged), we who exist in 3 dimensions experience the sphere as a single, undivided object of 'pure curvature': an entity of perfect roundness for which the terms 'slice', 'cross-section', and 'division of unit' have no meaning. What is it like to be on the surface of a sphere? As we've mentioned, being on a sphere such as the surface of the earth means travelling in any direction - and as far as you want - on its 2-dimensional surface, and never coming to a boundary. There is an important aspect to traversal across the surface of a sphere, however, that has not yet been pointed out: no matter where on the surface of the sphere you go, you will always experience being in the center of a flat 2-dimensional circular area. This occurs, of course, because the sphere is an object of 'pure curvature': its shape is observed to be the same from any point on its surface, from any direction of observation on that point. It is because of this very property that every point on the surface of a sphere could be said to be a potential "center" to those on its surface, in the sense that every point puts the subject in the center of what he perceives to surround him. In physical reality, however, and to those outside the surface of the sphere, the only real 'center' is the centerpoint of the sphere itself.

Take note, also, that there happens to be a certain 'twist' to being on the surface of a sphere, that you're probably already aware of: when on the surface of a sphere, there is no way of knowing whether you are actually on a curved spherical surface, or in the center of a flat circular plane that extends outward, but never curves downward to form a sphere (as is the case with the top of a table). Having lived our entire lives on the surface of a sphere, none of this is new to us. The sphere we exist on is in fact a planet. To a Flatlander, however, as we've seen, a sphere happens to be a universe! What this means is that what is common knowledge to us, is to a Flatlander a topic of mystery. We who exist in 3 dimensions have no difficulty grasping the concept of the experience of always being in the center of a flat circle when on the surface of a sphere, regardless of our location on it. Given that a Flatlander cannot experience a sphere as an object of 'pure curvature' as we do, however, but only as "chopped up" into an array of circles in the form of a stack-diagram, how would we express this concept to a Flatlander?

Recall that in a previous section we witnessed the journey of a 2-dimensional flying saucer across the slices of a sphere. In these sequences the flying saucer begins at what looks like the center of the sphere, and then moves over to positions within the stack-diagram that bring the saucer away from its initial position, in effect leaving what appears to be the center of the sphere. Given what was discussed above, this appears to contradict the notion that states that the saucer would always be in the center! To be able to understand what is happening here, we must be aware that the perception of always being 'in the center' applies to the individual experience of the saucer: no matter where on the sphere the flying saucer travels, it will perceive itself as being 'in the center' of the 2-dimensional surface that surrounds it. The saucer appears to 'leave the center' simply because our view of the sphere remains the same throughout the entire sequence - in effect, when the saucer's location on the sphere changes, our view of the sphere is not modified in response to that change.

To portray to a Flatlander, then, the concept of always perceiving being 'in the center' of a surface of 'pure curvature' (the sphere) when the Flatlander is limited to the sphere in the form of the 'array of circles' that the sphere exists as in stack-diagram form, we apply part of the reasoning found in the previous paragraph. The apparent solution to this situation is to attempt to keep the flying saucer from leaving its placement on the location we understand to be the 'center' of the stack-diagram - the 'center' of the stack-diagram being the very top of the central slice. How, then, do we keep the saucer fixed in this position? To keep the saucer fixed in this position, we assume that whenever the saucer moves forward in any direction, our view of the sphere is at that moment 'updated'. As a result, the saucer never leaves what we understand to be the center of the stack-diagram: at all times we will observe the saucer to lie at the very top of the central slice. The row of slices we see after each 'update' is a row of slices displaying the surface of the sphere as it appears from a new angle.

In all of the sequences presented so far, we have observed the surface of the sphere from a fixed position as the saucer's position changes - in which the saucer appears to us to move. In terms of the arrangement we are discussing here, however, it is the saucer's position that is fixed, and the mapping on the surface of the sphere (as it appears spread across the slices of the stack-diagram) that appears to move as it changes. How is the saucer's fixed position on the central slice of the stack-diagram related to the experience of always being 'in the center' of one's position on the surface of a sphere? One's experience of being on the surface of a sphere is of a 'fixed' nature in the sense that though a subject's location on a sphere may change (presenting new surroundings to the subject), the subject's experience of always being in the center of the environment he perceives occupying will at all times remain a constant occurrence. With this in mind, consider the notion that a subject on the surface of a sphere in a sense never moves: from the subject's point of view, it's not he himself that moves (from his constant position in the center of his surroundings), but rather his surroundings that move (passing him by as he moves forward)!

With this in mind, take note that a subject's conception of his location on a sphere is based entirely upon the surroundings the subject perceives occupying. If, in fact, these surroundings did not exist (leaving only a blank sphere), there would be no way to designate location on the sphere: no references would exist as a means for those on the surface of the sphere to orient themselves based upon their surroundings, and as a result there would be no way to express the uniqueness of any point on the surface of the sphere from any other point. It would be as if every point had the potential to be every other point! This property, of course, would be the result of the sphere being an object of 'pure curvature'.

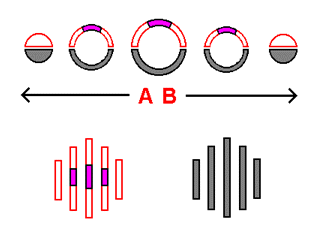
The top of the illustration presented to the right displays the 2-dimensional spherical universe that we have worked with earlier, in stack-diagram form. As you can see, the familiar 2-dimensional flying saucer, in the form of its cross-sections, is placed on the very top of the central slice (the location we understand to be the 'center' of the stack-diagram). You may also observe that the top halves of the slices of the sphere are highlighted. The highlighted halves represent the "side" of the 2-dimensional universe that the flying saucer is on - in this case, the top half. If the sphere in the stack-diagram were a globe, the 'northern hemisphere' of the globe would be highlighted. Of what importance is the flying saucer's "side"? It represents the outermost 'edge' of the 2-dimensional circular area visible to the saucer - the boundary past which vision from the saucer's position is not possible. The reasoning behind such a border lies in the fact that there is a limit to how far we can see outward toward the horizon from our own location on the earth: rather than seeing 'all the way around', what we can see is limited by distance. As with the surface of the earth, everything on the saucer's "side" appears completely flat to the saucer, lacking any hint of curvature. Underneath the stack-diagram are 2 circular formations. These are flat views of the 2 "sides" - the 'visible' side and the 'unseen' side. These views represent how the 2-dimensional universe represented in the stack-diagram would be perceived by a subject within its surface such as the saucer. As you can see, the cross-sections of the saucer are included in the flat view of the 'visible' side, occupying what would be the north pole if the 'visible' side were the northern hemisphere of a globe. The material just presented represents a Flatlander's basic conception of how perception of the surface of a sphere occurs.

As we've learned, our best conception of a hypersphere exists "chopped up" into an array of spheres (as a stack-diagram is arranged). This is a very limited, awkward view of a hypersphere, however: in 4 dimensions, the hypersphere is a single, undivided object of 'pure curvature': an entity of perfect roundness for which the terms 'slice', 'cross-section', and 'division of unit' have no meaning. We know that as a result of a fundamental property of the hypersphere, a spaceship on the surface of a hypersphere can travel in any direction, and as far as desired, and never come to a boundary. Given this information, consider an important aspect to traversal across the surface of a hypersphere - an aspect not yet mentioned, and similar in nature to what was pointed out earlier concerning the sphere: this aspect states that no matter where on the surface of a hypersphere you go, you will always experience being in the center of a 3-dimensional spherical volume. This occurs because the hypersphere is an object of 'pure curvature': its shape is observed to be the same from any point on its surface, from any direction of observation on that point. It is because of this very property that every point on the surface of a hypersphere could be said to be a potential "center" to those on its surface, in the sense that every point puts the subject in the center of what he perceives to surround him. In physical reality, however, and to those outside the surface of the hypersphere, the only real 'center' is the centerpoint of the hypersphere itself. With this in mind, take note that there exists a 'twist' to existing on the surface of a hypersphere, quite similar in nature to the 'twist' involved with being on the surface of a sphere: when on the surface of a hypersphere, there exists no means whatsoever of being certain as to whether you are inside of what is simply the spherical volume of a giant sphere, or whether your experience of occupying the center of a spherical volume is in fact a view from a point on the surface of a hypersphere! Given, however, that our understanding of a hypersphere exists at best "chopped up" into an array of spheres as a stack-diagram is arranged (rather than as an object of 'pure curvature'), how would we be able to grasp the concept of always being in the center of a spherical volume, regardless of our location on the surface of a hypersphere?

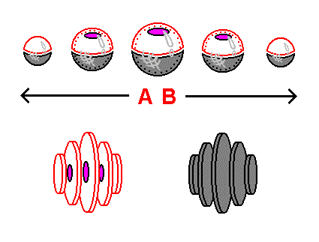The top of the illustration presented to the right displays the 3-dimensional hyperspherical universe that we have worked with earlier, in stack-diagram form. The familiar spaceship, in the form of its cross-sections, is placed on the very top of the central slice (the location we understand to be the 'center' of the stack-diagram). As you can see, the top halves of the slices of the hypersphere are highlighted. The highlighted halves represent the "side" of the 3-dimensional universe that the spaceship is on - in this case, the top half. The spaceship's "side" represents the outermost 'edge' of the 3-dimensional spherical volume visible to the spaceship - the boundary past which vision from the spaceship's position is not possible. Everything on the saucer's "side" appears completely normal, lacking any hint of any kind of distortion that curvature would cause. Underneath the stack-diagrams are the flat views of the 2 "sides" - the 'visible' side and the 'unseen' side. These views represent how the 3-dimensional universe represented in the stack-diagram would be perceived by a subject within its surface such as the spaceship. As you can see, the cross-sections of the spaceship are included in the flat view of the 'visible' side, emphasizing the presence of the very spherical volume that the spaceship perceives occupying the center of.

Document, if you will, the spaceship's position in the center of the stack-diagram (at the top of the stack-diagram's central slice). Let the spaceship's observed placement in the center of things convey the concept of how the spaceship always perceives being in the center of its surroundings, regardless of the spaceship's location on the hypersphere. However, if the spaceship moves, it leaves what we perceive the center of the stack-diagram to be. In order to see the hypersphere represented by the stack-diagram for the element of 'pure curvature' that it is, we must prevent the spaceship from leaving its position at the center of the stack-diagram. To perform this feat, we give the spaceship a fixed position: whenever the spaceship moves forward in any direction from its position at the top of the central slice of the stack-diagram, our view of the hypersphere is at that moment 'updated'. As a result, the spaceship never leaves what we understand to be the center of the stack-diagram: at all times we will observe the spaceship to lie at the very top of the central slice. The row of slices we see after each 'update' is a row of slices displaying the surface of the hypersphere as it appears from a new angle. If desired, you can picture the change that occurs among the slices of the stack-diagram to be projected onto the slices of the flat views, and in doing so obtain a more straightforward idea as to the surroundings that the spaceship in the stack-diagram experiences occupying.

In all of the sequences presented so far, we have observed the surface of the hypersphere from a fixed position as the spaceship's position changes - in which the spaceship appears to us to move. In terms of what we are considering now, however, it is the spaceship's position that is fixed, and the mapping on the surface of the hypersphere (as it appears spread across the slices of the stack-diagram) that appears to move as it changes. How is the spaceship's fixed position on the central slice of the stack-diagram related to the experience of always being 'in the center' of one's position on the surface of a hypersphere? One's experience of being on the surface of a hypersphere is of a 'fixed' nature in the sense that though a subject's location on a hypersphere may change (presenting new surroundings to the subject), the subject's experience of always being in the center of the environment he perceives occupying will at all times remain a constant occurrence. With this in mind, consider the notion that a subject on the surface of a hypersphere in a sense never moves: from the subject's point of view, it's not he himself that moves (from his constant position in the center of his surroundings), but rather his surroundings that move (passing him by as he moves forward)!

With this in mind, take note that a subject's conception of his location on a hypersphere is based entirely upon the surroundings the subject perceives occupying. If, in fact, these surroundings did not exist (leaving only a blank hypersphere), there would be no way to designate location on the hypersphere: no references would exist as a means for those on the surface of the hypersphere to orient themselves based upon their surroundings, and as a result there would be no way to express the uniqueness of any point on the surface of the hypersphere from any other point. It would be as if every point had the potential to be every other point! This property, of course, would be the result of the hypersphere being an object of 'pure curvature'. The material just presented represents our basic conception of how perception of the surface of a hypersphere occurs. In the next section we attempt to visualize extension perpendicular to the surface of the hypersphere.