The Hypersphere and Gravity

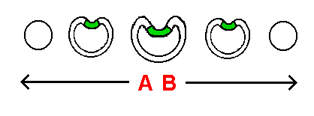
The theory of relativity states that a concept known as curved space is responsible for the action of gravity. 'Curved space' can be described as the physical warping of the surface surrounding a body due to the body's mass. The mass of the body causes the body to 'sink down' into the surface, surrounding the body with a downhill 'curved sag' that brings the body down to a level below the level of the rest of the surface. The stack-diagram below to the right - portraying the 2-dimensional spherical universe that we are familiar with - displays a 2-dimensional planet surrounded by the distinct 'curved sag' that we call curved space. This curved sag shown spread across the slices of this stack-diagram represents a 3-dimensional curvature of a 2-dimensional surface. The curvature is 3-dimensional in the sense that the task of physically warping ('curving') a 2-dimensional surface involves 3 dimensions: the first 2 dimensions of the arrangement involve the 2 dimensions associated with the surface itself. The extra dimension - the third dimension - allows the surface to be bent, shaped, and distorted in ways not expressable as of the 2 dimensions within the surface. Because a curved sag formed by such a means is, as stated, a curvature of a 2-dimensional surface into the third dimension, the curved sag itself can be labeled appropriately as a 3-dimensional entity.

As you can see, our view of this 3-dimensional curved sag is somewhat limited, given the fact that we can only observe it in the form of its cross-sections (the 2-dimensionally curved sags that exist within the individual 1-dimensional surfaces of the slices of the stack-diagram). This limitation, however, is not a problem for us: upon moving the slices of the 2-dimensional universe over to their 3-dimensional positions behind and in front of the central slice, we can then mentally "combine" these divided units into a single entity. Afterward, we can easily picture the 3-dimensional contour of the shape of the curved sag. Doing so allows us to see the 3-dimensional curved sag for the element of 'pure curvature' that it is - an element existing beyond 'cross-sections' and 'slices'. Like the curved sag, the 2-dimensional planet lying at the bottom of the curved sag is divided into cross-sections: as you can see, the 2-dimensional planet is itself curved along with the 3-dimensional curvature of the curved sag. The outer surface of the 2-dimensional planet, furthermore, existing within a curved 2-dimensional surface in the way that it does, is surrounded by the curved sag on all sides. The manner in which the cross-sections of the planet increase and then decrease in size, in turn, is a direct result of the circular shape of the planet.

The stack-diagram below to the right - portraying a 3-dimensional hyperspherical universe - extends our knowledge of the concept of 'curved space' by attempting to portray the very 4-dimensional curvature associated with the theory of relativity. The 'curved sag' shown spread across the slices of this stack-diagram represents a 4-dimensional curvature of a 3-dimensional surface. The curvature is 4-dimensional in the sense that the task of physically warping ('curving') a 3-dimensional surface involves 4 dimensions: the first 3 dimensions of the arrangement involve the 3 dimensions associated with the surface itself. The extra dimension - the fourth dimension - allows the surface to be bent, shaped, and distorted in ways not expressable as of the 3 dimensions within the surface. Because a curved sag formed by such a means is, as stated, a curvature of a 3-dimensional surface into the fourth dimension, the curved sag itself can be labeled appropriately as a 4-dimensional entity.

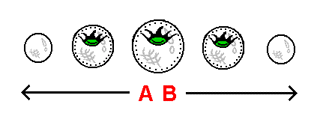As you can see, our view of this 4-dimensional curved sag is somewhat limited, given the fact that we can only observe it in the form of its cross-sections (the 3-dimensionally curved sags that exist within the individual 2-dimensional surfaces of the slices of the stack-diagram). This limitation occurs for the same reason that we cannot experience a hypersphere as a single entity, but only as "chopped up" into an array of spheres. There is, however, a means by which we can attempt to overcome this obstacle: we are to picture moving all of the slices of the 3-dimensional universe over onto the central slice, so that all of these slices occupy the 'same space' as the central slice. We are then to imagine the cross-sections of the 4-dimensional curved sag to themselves "overlap" in the same manner that the slices of the 'compressed hypersphere' in a previous section were considered to "overlap". Once in their positions, we are to imagine the individual, separate 2-dimensional surfaces of these 3-dimensional curved sags to "combine" into a single entity (in the same manner that the slices of the 'compressed hypersphere' were observed to "combine" into a single entity). The result is an undivided 4-dimensional curved sag that we are to observe as an element of 'pure curvature' - an element existing beyond 'cross-sections' and 'slices'. Like the curved sag, the 3-dimensional planet lying at the bottom of the curved sag is divided into cross-sections: as you can see, the 3-dimensional planet is itself curved along with the 4-dimensional curvature of the curved sag. The outer surface of the 3-dimensional planet, furthermore, existing within a curved 3-dimensional surface in the way that it does, is surrounded by the curved sag on all sides. The manner in which the cross-sections of the planet increase and then decrease in size, in turn, is a direct result of the spherical shape of the planet.

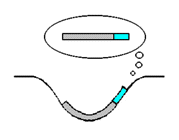Take note that though this 'curvature' of space is a very real 'warping' of the shape of a surface, its physical presence is not in fact detectable from within that surface. The illustration to the right demonstrates this notion by displaying a representation of a 1-dimensional creature (the short light blue segment) standing on a 1-dimensional planet (the larger curved segment). As you can see, the situation takes place from within a curved surface. The illustration, it so happens, presents the 1-dimensional creature's conception of his placement within that surface - which, as you can see, lacks the curvature that we observe. The same could be said to apply to us: just as the creature shown here experiences his world as being completely 1-dimensional when in reality his world happens to be curved into the second dimension, we experience our world as being completely 3-dimensional when in reality our world happens to be curved into the fourth dimension.

Why do objects fall? The typical explanation states that the objects that are falling do so because they are "attracted" to another object in exactly the same way magnets are attracted to each other: gravity is a mysterious 'pulling force' that is "built in" to the way objects work, and cannot be explained beyond that. It is this approach to gravity that Newton is famous for and represents our basic concept of gravity. Though this approach accurately predicts the behavior of gravity, it does not explain what gravity is or why gravity does what it does. The purpose of this section is to address these issues, and in the process provide an explanation as to why objects fall.

'Curved space' is not the only thing that the theory of relativity associates with the action of gravity. The theory of relativity associates motion with the action of gravity. In fact, the theory of relativity states that the action of gravity and the effects of motion are 2 ways of thinking of the same thing! Einstein's famous elevator thought experiment addresses the issue of how gravity and motion are related. In this thought experiment there is an elevator travelling though outer space at a high speed. A person in the elevator is pressed to the floor of the elevator as a result of the physical force of the motion, in the same way that we would imagine gravity to 'pull' someone to a floor. The conclusion of this thought experiment is that nothing actually falls: a ball 'dropped' within the elevator appears to fall, but in reality what happens is the floor of the elevator moves up to a ball that itself was stationary the whole time! What this means is that when we drop a ball and it falls to the ground, it wasn't the ball that moved (down to the ground), but the ground that moved (up to the ball)! Does this mean that the earth is expanding?

This would seem to be the logical conclusion given the reasoning of the elevator thought experiment. Though this assumption is not entirely accurate, it is a step in the right direction: it is not an 'expanding earth', but rather the expansion of the universe, you see, that provides the motion necessary for the earth to come up to meet the ball - the earth is carried along with the universe as the universe expands! The concept of an "expanding earth" as the source of the motion behind the action of gravity, though based on the reasoning of a valid argument, is in reality 3-dimensionally impossible: to be able to move up to a ball dropped anywhere on the earth's surface, the earth would have to be expanding outward in all directions - a feat that upon being attempted would rip the earth apart! The question that we must ask, then, is that of how the earth could travel in a single direction, and yet at the same time address all points on its 2-dimensional spherical surface. There exists no 3-dimensional means by which such a feat can be performed. To physically envision the process of the earth moving up to a ball dropped onto the ground anywhere on its surface, we must approach the situation from a 4-dimensional point of view.

The stack-diagram of a 3-dimensional hyperspherical universe that is presented below to the right represents such an approach. The expansion of this universe - the very expansion that would make it possible for the earth to move up to a dropped ball - is indicated by means of the arrows surrounding the hyperspherical slices. Our best means of understanding how the 2-dimensional spherical surface of the earth could move up to a ball dropped onto any point on its surface exists in the form of what we will refer to as the 4-dimensional curvature of the earth. Take note, firstly, that we cannot directly visualize a 4-dimensionally curved earth. That is, we cannot experience a 4-dimensionally curved earth as a single entity (in the same way that we cannot experience a hypersphere as a 'single entity' but only as "chopped up" into an array of spheres). What we can comprehend, however, is a 4-dimensionally curved earth as it exists spread across multiple 3-dimensional planes. To visualize a 4-dimensionally curved earth, we divide the earth into circular cross-sections, and then assign each cross-section to its own 3-dimensional plane (as has already been done in the stack-diagram below to the right). We are then to modify the cross-sections by '3-dimensionally curving' the circle on each and every 3-dimensional plane: we curve the circle upward so that the 1-dimensional circular edge of the circle is raised up above the rest of the circle (putting the centerpoint of the circle at the very bottom). The resulting formation will resemble a bowl - a 3-dimensionally curved circle. This curvature of circular cross-sections, like the cross-sections themselves, is observable within the stack-diagram.

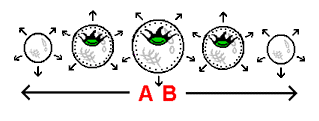This presents to us our best conception of a 4-dimensionally curved sphere - an array of 3-dimensionally curved circles. Because the 1-dimensional circular edge of the curved circle making up each cross-section is "raised up" above what is understood to be that circle's centerpoint (which lies at the very bottom), we in turn assume that when these circular cross-sections "combine" to form a 4-dimensionally curved earth, the 2-dimensional spherical surface of the earth is equally considered to be "raised up" above its own 3-dimensional centerpoint, which, like the centerpoint of the curved circle described, is a centerpoint that lies at the very bottom of the curved entity of which it is a part. The description of a 4-dimensionally curved earth just given represents our basic understanding as to the shape of an earth as it would lie at the bottom of a 4-dimensional curved sag. The placement of a 4-dimensionally curved earth at the bottom of such a curved sag is displayed, as you can see, in the stack-diagram. Assuming that the earth is at the bottom of such a curved sag, we would observe the expansion of the universe to always bring the surface of the earth up to meet a dropped ball as it should, no matter where along the 4-dimensional curved sag the ball is dropped. In the material to be addressed next, we will cover topics that will allow us to better understand the details of how the earth moves up to objects dropped onto its surface. The entire 3-dimensional surface of our universe, then, is in fact the 'elevator' we've been speaking of - the 'elevator' that provides the very motion that makes gravity possible. How do 'curved space' and the effects of motion work together to produce the effect we call gravity?

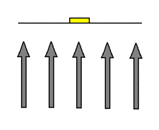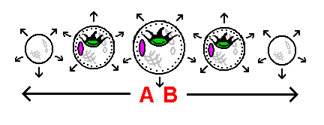
Displayed to the left is a stack-diagram of the hyperspherical 3-dimensional universe we have been working with. Included are the cross-sections of a spherical planet and the 4-dimensional 'curved sag' that surrounds it. On the left side of the 3-dimensional universe, divided into cross-sections in the same manner as the planet is divided into cross-sections, is an object we are labeling as a floating 'space rock'. Just as our own universe is in a state of constant expansion, we are to imagine the hyperspherical universe in this stack-diagram to be in a state of constant expansion. This expansion is represented in the stack-diagram by means of the arrows surrounding the slices. As a result of this constant expansion, both the planet and the space rock are carried outward along with the hyperspherical surface as it expands. This in fact puts the planet in the 'motion' required of it to move up to objects that are dropped onto its surface. The space rock, itself also being carried outward by the expansion of the hyperspherical surface, can be considered to be in a state of motion equal to that of the planet. The space rock, though in motion in terms of the outward expansion of the hyperspherical surface (motion of the surface itself), is not affected by the effects of gravity (motion that occurs within the surface). Why not? In order for gravity to occur, the effects of motion must take place in the presence of curved space. Because the space rock is not in the presence of curved space, it is in a state of what we call weightlessness: any and all motion of the space rock within the hyperspherical surface will always be the result of a force other than gravity. The bottom illustration to the left shows a simplified illustration of how being "pressed down" upon by the effects of motion has no effect on an object not in the presence of curved space.

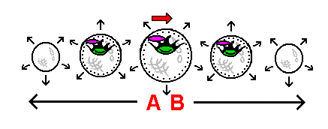
In the stack-diagram to the left, the space rock that was far from the planet in the stack-diagram of the hyperspherical universe shown above has now been placed in the very 'curved space' that surrounds the planet. There exists essentially 2 ways, take note, that an object can come into a state of being overtaken by curved space: firstly, an object can drift into the curved space from weightlessness. Secondly, an object can simply be dropped. Once within the grip of the curved space (and unaware of the rising planet at the bottom of the 4-dimensional curved sag) a second element comes into action: the outward motion of the hyperspherical universe. As a direct result of the physical force of expansion "pressing down" upon the space rock, the space rock is 'pushed' into the curvature of the curved sag as the planet rises toward it. In response, the space rock "slides" toward the planet as a result of being pushed in that direction by the rising curvature.

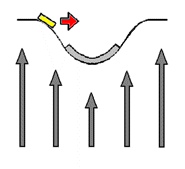
This is the process we call "falling" - gravity-related motion toward a massive body. Its occurrence in the stack-diagram is designated by the red arrow. Unless affected by forces other than gravity, the space rock will continue along its path until met from below by the planet. The bottom illustration to the left shows a simplified illustration of the process of gravity as it has been described, showing a simple portrayal of how the effects of motion take action in the presence of curved space. The illustration makes clear the manner in which an object "slides" toward a massive body as a result of being 'pushed' into the curvature surrounding the body. As you can see by what was described here, gravity is not a mysterious 'pulling force', but is rather a clearly defined process that can be understood in terms of very simple, straightforward concepts. In the next section we will see how time and the expansion of our hyperspherical universe are related.