A hypersphere is to a sphere,
what a sphere is to a circle.

Recall ages ago, when most people believed that the earth was flat. Some thought that they would "fall off the edge" of the earth if they went out too far. Little did they know, that if they kept on going, they could possibly end up where they started, having experienced the entire trip as being in a straight line! No matter how far the subject travels (by boat, train, or plane), he will never come to a boundary: there is no "edge" to fall off of!! It is because the earth exists on the surface of a sphere that these properties hold true. Let us take this a step further.

Having launched from the earth is a rocket ship that is travelling out into space. Its mission is to continue outward in a straight line in its current direction until it reaches the "outer edge" of the universe. When will the rocket ship reach the outer edge of space? In the previous example we find a similar situation: the concern of "falling off the edge" of a flat earth - an earth that in reality has no "edge" to fall off of. What if the same were true for the universe? Our rocket ship moving outward into space would not only fail to encounter an "outer edge" to the universe, but could possibly end up where it started, having experienced the entire trip as being in a straight line! No matter how far the rocket ship travels through space, it will come across no boundary of any kind. These properties would hold true if the universe existed on the surface of a hypersphere in the same way that the earth exists on the surface of a sphere.

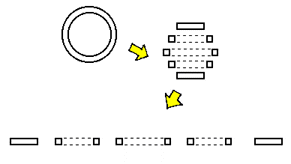
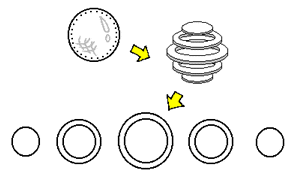
How would we picture a hypersphere? The key to approaching something of the fourth dimension is by means of the tool of analogy: we rely upon corresponding lower-dimensional structures as the means by which their 4-dimensional analogue is constructed. A circle is a 2-dimensional object. When cut into slices, as is done in the top illustration to the right, we find that a circle is in essence an array of segments: the outer slices (the 'poles') are solid segments and are smallest. The inner slices are larger hollow segments that increase and then decrease in size. A sphere, as shown in the bottom illustration to the right, is a 3-dimensional object. When cut into slices, we find that a sphere is in essence an array of circles: the outer slices (the 'poles') are solid circles and are smallest. The inner slices are larger hollow circles that increase and then decrease in size. Having obtained the knowledge we have so far, we now possess the ability to bring these lower-dimensional structures "up a notch" through analogy to envision a hypersphere.

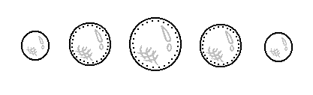We cannot directly visualize a hypersphere for the very reason that it is a 4-dimensional object. What we can visualize, however, is a hypersphere in the form of 3-dimensional slices (as is displayed to the left). A hypersphere is in essence an array of spheres: the outer slices (the 'poles') are solid spheres and are smallest. The inner slices are larger hollow spheres (marked as hollow by dotted lines) that increase and then decrease in size. This would represent our basic conception of the hypersphere. In the next section we will attempt to construct a '4-dimensional plane' with which we can contain the slices of the hypersphere we've just identified.